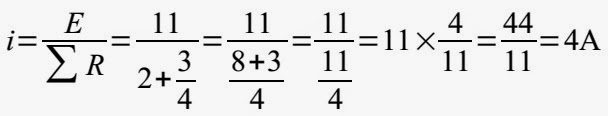Resolução da prova mensal do 4º bimestre - 2ª série - 2014

Para acessar o arquivo com a resolução da prova mensal basta clicar no link abaixo.

Prova Mensal de Física - 4º bimestre - 2ª série

Resolução da prova mensal do 3º bimestre - 3ª série 2014

Para acessar o arquivo com a prova resolvida basta clicar no link abaixo:

Resolução da prova mensal do 3º bimestre - 3ª série 2014

Resolução da prova mensal da 2ª série - 3º bimestre 2014

Para acessar o arquivo com a resolução comentada da prova mensal clique no link abaixo:

Resolução da prova mensal da 2ª série - 3º bimestre 2014

Resolução da prova mensal de Física - 1ª série - 3º bimestre.

Clique no link abaixo para visualizar a resolução da prova.

Resolução da prova mensal de Física - 1ª série - 3º bimestre.

Movimento de uma partícula eletrizada em um campo magnético uniforme.

(ITA)– Uma partícula com carga q e massa M move-se ao longo de uma reta com velocidade v constante numa região onde estão presentes um campo elétrico de 500V/m e um campo de indução magnética de 0,10T. Sabe-se que ambos os campos e a direção de movimento da partícula são mutuamente perpendiculares. A velocidade da partícula é:

a) 500m/s.
b) constante para quaisquer valores dos campos elétrico e magnético.
c) (M / q) 5,0 x 10³m/s.
d) 5,0 x 10³m/s.
e) faltam dados para o cálculo.

Resolução:

Para que a partícula mova-se com velocidade constante ao longo de uma reta (MRU) a força resultante sobre ela deve ser igual a zero (condição de equilíbrio). Sendo assim as forças magnética e elétrica precisam ter mesma direção, sentidos opostos e mesmo módulo.

                                           Força magnética = Força elétrica (carga x campo elétrico)

                                            q.v.B.sen θ = q.E
                                              v.B .sen 90° = E
                                              v.0,10.1 = 500
                                              v = 500/0,10
                                              v = 5000m/s
O item (b) está incorreto, pois alterando-se os módulos dos campos (magnético ou elétrico) é desfeito o equilíbrio das forças, alterando as condições propostas na questão (MRU). 

Resolução da prova bimestral da 3ª série - 2º bimestre

Para acessar o arquivo com a resolução da prova clique no link abaixo.
(Apenas um dos tipos de prova está resolvida)

Resolução da prova bimestral da 3ª série - 2º bimestre

Resolução da prova bimestral da 2ª série - 2º bimestre

Clique no link abaixo para ter acesso à resolução da prova bimestral da 2ª série.

Resolução da prova bimestral da 2ª série - 2º bimestre

Resolução da prova bimestral da 1ª série - 2º bimestre

Clique no link abaixo para ter acesso à resolução da prova bimestral da 1ª série.

Resolução da prova bimestral - 1ª série - 2ºbimestre

Estática do corpo extenso

(FUVEST)– A figura mostra uma barra homogênea AB, articulada em A, mantida em equilíbrio pela aplicação de uma força F em B. Qual o valor do ângulo para o qual a intensidade de F é  mínima?

Resolução:
Para que a barra mantenha-se em equilíbrio, o somatório dos torques sobre ela deve ser nulo.
Sobre a barra, além da força F, atua o peso da mesma que atua sobre seu centro de gravidade que está no seu ponto médio (barra homogênea).  Pode-se determinar os torques produzidos pelas forças Peso e F a partir de suas componentes retangulares. Veja a figura abaixo:

 A força peso (P) produz torque no sentido horário sobre a barra através de sua componente P_N e a força F produz torque no sentido anti horário através da componente  F_N. 
A componente P_N é obtida pela equação:  P_N = P . cos 30°

A componente F_N é obtida pela equação: F_N = F. sen (180 - α).
Para que a barra esteja em equilíbrio:    M_P =  M_F  

                                  P_N . AB/2 =  F_N . AB
                                  P . cos 30º /2 = F . sen (180 - α)

 Para a conclusão da questão é importante relembrarmos um conceito básico da trigonometria. O seno de um ângulo para o intervalo 0 ≤ α ≤ 180° assume valores no intervalo  0 ≤ sen α ≤ 1.
Para que a Força F tenha valor mínimo, o sen (180 - α) deve assumir o valor máximo que é 1.

Temos então que :  sen (180 - α) = 1 (lembre-se que sen 90° = 1)
Portanto   180 - α = 90°
                 180 - 90 = α
                  α = 90° 

Geradores elétricos

No circuito da figura, o reostato AB é munido do cursor C, sendo a resistência entre A e B igual a 40Ω . Qual a corrente no gerador quando o cursor está em B? Em que posição deverá ser colocado o cursor para que a corrente no gerador seja a metade daquela encontrada na situação anterior?

Resolução:

1ª questão: 
Qual a corrente no gerador quando o cursor está em B?

Estando o cursor em B, temos o resistor de 20Ω em situação de curto circuito. 

Dessa forma o circuito fica reduzido à força eletromotriz do gerador (20V) e ao resistor de 10Ω.
Utilizando a Lei de Pouillet encontramos:
                                                       i = E /∑ r 

                                                       i = 20 / 10
     
                                                       i = 2A
2ª questão: 
Em que posição deverá ser colocado o cursor para que a corrente no gerador seja a metade daquela encontrada na situação anterior?
Para esse caso sabemos que a corrente elétrica no gerador deverá ser igual a 1A (metade da corrente encontrada na questão anterior).  O cursor deve ser posicionado em um ponto da resistência entre A e B.

Utilizando a Lei de Pouillet é possível determinar o valor de R_p(associação dos resistores  R_BC e 20Ω) :

Agora é possível determinar a resistência  R_BC obtida pela posição do cursor no reostato:

Queda livre

Em um local onde o efeito do ar é desprezível e g = 10m/s², um vaso de flores cai, a partir do repouso, da mureta de um prédio e gasta 0,10s para passar diante de uma janela de altura 1,25m.
De que altura h, acima da extremidade inferior da janela, caiu o vaso?

Resolução:
Observe a figura abaixo:

 O vaso leva um tempo (T - 0,10)s para chegar à parte mais alta da janela e percorre uma distância (h - 1,25)m. Substituindo na equação do deslocamento no MUV temos: 

Propriedades gráficas do MUV

(FUVEST)– Dois trens, A e B, fazem manobra em uma estação ferroviária deslocando-se paralelamente sobre trilhos retilíneos. No instante t = 0s eles estão lado a lado. O gráfico representa as velocidades escalares dos dois trens a partir do instante t = 0s até t = 150s, quando termina a manobra.

A distância entre os dois trens no final da manobra é:
a) 0m                          b) 50m                     c) 100m              d) 250m                   e) 500m

Resolução:

O gráfico mostra que os trens deslocam-se sempre em sentidos opostos no intervalo de 0 a 150s. 

Inicialmente o trem A tem velocidade positiva até inverter o sentido no instante 50s. O trem B tem velocidade negativa inicialmente até inverter o sentido também no instante 50s.  

A área sob o gráfico da velocidade em função do tempo nos fornece o deslocamento do móvel. 

Portanto basta calcular o deslocamento de cada trem no intervalo de 0 a 150s. (Não esquecer que áreas abaixo do eixo do tempo representam deslocamentos negativos).

Deslocamento de A = (50.5)/2 + (-5.50)/2 + (-5.50)/2

Deslocamento de A = 125 - 125 - 125 =  - 125 m

Deslocamento de B =  (- 5.50)/2 + (5.50)/2 + (5.50)/2

Deslocamento de B = -125 + 125 + 125

Deslocamento de B = 125 m

Temos que o trem A deslocou-se 125 metros para um sentido e o trem B 125 metros no sentido contrário. Portanto a distância entre os trens é (125 + 125) de 250 metros. 

Propriedades gráficas - Movimentos

(FUVEST)– Na figura, estão representadas as velocidades escalares, em função do tempo, desenvolvidas por um atleta, em dois treinos, A e B, para uma corrida de 100m rasos.

Com relação aos tempos gastos pelo atleta para percorrer os 100m, podemos afirmar que, aproximadamente,

a) no B levou 0,4s a menos que no A.
b) no A levou 0,4s a menos que no B.
c) no B levou 1,0s a menos que no A.
d) no A levou 1,0s a menos que no B.
e) no A e no B levou o mesmo tempo.
Resolução:

Sabe-se que a área sob o gráfico da velocidade em função do tempo é numericamente igual ao deslocamento do móvel. Não temos o tempo de corrida para nenhum dos dois treinos (A e B), porém temos o deslocamento do atleta que é de 100 metros. Este valor representa a área sob cada gráfico (A e B). Para o treino A temos:

 

A área (100) do trapézio é igual à soma da área do triângulo com a área do retângulo:

                           

Para o treino B temos:

A área (100) do trapézio é igual à soma da área do triângulo com a área do retângulo:

Pode-se perceber que no treino A, o atleta foi aproximadamente 0,4s mais rápido que no treino B.

Curva característica de um gerador

(F.M. JUNDIAÍ) – Um gerador (E, r) e um resistor R constituem o circuito elétrico abaixo. As curvas características destes aparelhos estão representadas no gráfico a seguir.

(I) A intensidade de corrente é i = 5A.
(II) A f.e.m. do gerador é 20V.
(III) A tensão no resistor é 10V.
(IV) A resistência do resistor é igual a 2 .
(V) O gerador tem resistência interna (r) numericamente igual a R.

Resolução:
(I) A intensidade de corrente é determinada pela Lei de Pouillet. Porém não são conhecidos os valores das resistências R e r. A resistência R do resistor pode ser obtida pela expressão da 1ª Lei de Ohm:
                                         U = R.i
                                         10 = R.5
                                         R = 10/5
                                         R = 2 Ω
O ponto onde a curva característica do gerador intercepta o eixo da intensidade de corrente indica a corrente de curto circuito (i _cc ). Portanto nesse caso temos i _cc = 10A. Quando está em curto circuito, o gerador não disponibiliza nada de tensão para o circuito, portanto U = 0. Veja as indicações no gráfico abaixo:

Utilizando a equação do gerador (U = E - r.i), pode-se determinar o valor da resistência interna r:

                                   0 = 20 - r.10

                                   10.r = 20

                                        r = 20/10

                                        r = 2 Ω

Agora é possível determinar a intensidade da corrente no circuito dado, utilizando-se a Lei de Pouillet:

 Portanto o item (I) está correto.

(II) Correto. Veja o gráfico acima.

(III) A tensão no resistor pode ser obtida pela equação do gerador (U = E - r.i). Como visto acima, a corrente elétrica no circuito é de 5 A.

                                U = 20 - 2.5

                                U = 20 - 10

                                U = 10 V

Portanto o item (III) também está correto.

(IV) Correto. Ver cálculo no item (I).

(V) Correto. Ver cálculo no item (I). R = 2 Ω e r = 2 Ω.

  

Resolução da prova sobre cinemática escalar e vetorial

Para acessar o arquivo com a resolução da prova use o link abaixo:

Resolução da prova mensal do 2º bimestre da terceira série.

Gráficos do MUV II

(UDESC)– No gráfico a seguir, representamos a posição (espaço) de uma partícula, que descreve um movimento retilíneo uniformemente variado, em função do tempo.

a) Determine, para o movimento da partícula, a velocidade escalar inicial V₀ e a aceleração escalar .
b) Construa o gráfico da velocidade escalar em função do tempo.

Resolução:

a) O vértice da parábola mostra o instante e o local onde ocorre a inversão do sentido do movimento. Portanto, pelo gráfico acima, sabemos que a partícula inverte o sentido do seu movimento no instante t = 2s e na posição s = - 1m. No instante da inversão do sentido do movimento sua velocidade é igual a zero. Podemos, considerando o intervalo de zero a 2s, determinar a velocidade inicial da partícula:

 A aceleração escalar pode ser determinada pela equação:

                                              v = v ₀  + γ.t
                                              0 =  - 4 + γ.2
                                              4 = γ.2

                                               γ = 4/2

                                               γ = 2m/s²

b) Com os resultados determinados no item (a) pode-se construir o quadro de valores de v e t e representá-los no plano cartesiano.

t(s)	v(m/s)
0	- 4
1	- 2
2	0
3	2

Geradores elétricos e Lei de Pouillet

(MACKENZIE)– No circuito representado abaixo, a bateria é ideal e a intensidade de corrente i₁ é igual a 1,5A.

O valor da força eletromotriz E da bateria é:
a) 50V                   b) 40V                     c) 30V                d) 20V                        e) 10V
Resolução:

Inicialmente você deve observar o esquema e verificar se não há nenhum curto-circuto. Neste caso percebe-se que os resistores de 5 Ω e 8 Ω foram colocados em "curto" pelo condutor que liga suas extremidades. Quando isso acontece, os terminais do resistor apresentam o mesmo potencial elétrico. Dessa forma não há passagem de corrente elétrica por nenhum desses dois resistores. Então o circuito pode ser representado da seguinte forma:

Como a corrente elétrica que passa pelo resistor de 12 Ω é conhecida, podemos determinar a tensão neste resistor:

                                         U₁ =   R₁. i₁ = 12x1,5 = 18V
Os  resistores de 12 Ω e 4 Ω estão associados em paralelo, portanto possuem a mesma tensão (18V).
Assim é possível determinar a intensidade de corrente i₂ :
                                         U₂ =   R₂. i₂ 
                                         18 = 4. i₂
                                           i₂ =18/4 
                                           i₂ = 4,5 A
Pela 1ª Lei de Kirchhoff (lei dos nós) sabemos que a soma das intensidades de corrente que chegam a um nó é sempre igual à soma das intensidades de corrente que saem dele. Portanto:
                                        i =   i₁   +   i₂
                                        i = 1,5 + 4,5
                                        i = 6,0 A 
A resistência equivalente entre os resistores de 4Ω e 12Ω pode ser determinada pela razão entre o produto e a soma dos mesmos:

 

Agora o circuito pode ser reescrito como:

 

 Aplicando a Lei de Pouillet, é possível determinar a força eletromotriz do gerador:

 

  

Gráficos do MUV

O gráfico a seguir representa a velocidade escalar em função do espaço (coordenada de posição) para um atleta em uma corrida de 100m.

O atleta descreveu uma trajetória retilínea e, até a posição x = 20m, o movimento é uniformemente variado. Construa o gráfico da velocidade escalar x tempo desde a partida até o instan te em que o atleta cruza a linha de chegada.

Resolução:

O movimento é uniformemente variado até a posiçao x = 20m. Portanto é possível determinar o tempo gasto pelo atleta para percorrer os primeiros 20 metros. A velocidade inicial é 0 (zero) e a velocidade final é 43,2 km/h. Lembre-se que essa velocidade precisa ser convertida para m/s (43,2 / 3,6 = 12 m/s)

No percurso de 20 a 100 metros o atleta manteve a velocidade constante em 43,2 km/h (12m/s). Portanto trata-se agora de um movimento retilíneo uniforme. O deslocamento é Δs = 100 - 20 = 80 metros. O tempo gasto nesse percurso é:

                                                          Δs = v.t
                                                          80 = 12.Δt₂ 1
                                                          Δt₂ = 80/12 = 40/6 = 20/3 segundos
O tempo total para a prova é obtido pela soma dos tempos de cada percurso:
                                               Δt = 10/3 + 20/3 = 30/3 = 10 s

Construindo o gráfico v x t, temos:

Provas da OBF 2014 com gabarito oficial.

Para acessar as provas da Olimpíada Brasileira de Física - 2014 clique nos links abaixo:

Prova para alunos de 8º e 9º anos do Ensino Fundamental

Prova para alunos de 1ª e 2ª séries do Ensino Médio

Prova para alunos de 3ª série do Ensino Médio

Resolução da prova mensal sobre trocas e transmissão de calor - 2ª série

A resolução da prova mensal de Física do 2º bimestre está disponível no link abaixo:

Resolução da prova mensal do 2º bimestre - 2ª série.

Lei de Pouillet

(COVEST-PE) – Qual a diferença de potencial, em volts, entre os pontos A e B do circuito abaixo?

Resolução:

Primeiramente é importante observar que o circuito está aberto entre os pontos A e B. Isso significa que não há passagem de corrente elétrica pelo resistor de 2 Ω (próximo ao ponto B).
Feita essa observação, basta calcular a intensidade da corrente elétrica que percorre o circuito utilizando a lei de Pouillet:

 A d.d.p. entre os pontos A e B é a d.d.p. nos polos do gerador. Esta é a mesma d.d.p. a que está sujeito o resistor de 2 Ω (na parte superior do circuito). Pode ser calculada pela equação:
                                                            U = R.i
                                                            U = 2.2 = 4V

Gráfico de um gerador real

(PUC)– A figura mostra o valor da tensão nos terminais de um gerador real em função da corrente por ele fornecida. A resistência interna do gerador é de:
a) 0,5             b) 1,0            c) 2,0            d) 4,0            e) 6,0

Resolução:
Podemos pelo gráfico determinarmos dois pares de coordenadas (i; U) que são:
- intersecção com o eixo da tensão - A (0; 6)
- intersecção com o eixo da intensidade de corrente  - B(6; 0)
A equação do gerador real é:    U = E - r. i
Sendo que U = diferença de potencial entre os terminais do gerador.
                  E = força eletromotriz do gerador.
                  r = resistência interna do gerador.
                  i = intensidade de corrente que percorre o gerador.
Substituindo os pontos na equação do gerador, temos:
Ponto A:   6 = E - r.0
                 E = 6V

Ponto B: 0 = E - r.6   (porém a força eletromotriz foi determinada como 6V)
               0 = 6 - 6.r
               6.r = 6
               r = 6/6
               r = 1 Ω
 

Geradores elétricos em curto circuito

(CESGRANRIO)– Em qual (quais) das situações ilustradas abaixo a pilha está em curto-circuito?

a) somente em I                       b) somente em II                            c) somente em III
d) somente em I e II                e) em I, II e III

Resolução:

O curto-circuito ocorre quando o gerador tem seus polos interligados por um condutor de resistência nula ou desprezível. Tanto em (II) quanto em (III) existe uma resistência não nula entre as ligações dos dois polos do gerador. Apenas em (I) devido aos dois resistores terem sido colocados em curto pelo condutor central da associação em paralelo, o gerador está em curto-circuito. Veja a figura:

 

Velocidade relativa

Duas partículas, A e B, estão em movimento em uma mesma trajetória retilínea. No instante t = 0, a partícula B está à frente de A e a distância que as separa é D.

O gráfico a seguir representa as velocidades escalares de A e B, em função do tempo.

Esboce a representação gráfica que traduz como a distância dentre A e B varia com o tempo t.

Resolução:
O móvel B está à frente e possui uma velocidade maior que o móvel A.
A velocidade relativa entre os dois móveis é obtida por:
V_BA = V_B - V_A 
Podemos perceber que os gráficos de A e B são paralelos em qualquer ponto e que a diferença entre as velocidades é constante e igual a V₁. Considerando que a velocidade relativa é constante e que o móvel B (mais rápido) estava inicialmente à frente, pode-se concluir que a distância entre eles irá aumentar com o passar do tempo. Portanto o gráfico deverá ser representado por uma reta crescente (pois tem velocidade relativa constante e positiva) e ponto inicial (0; D).

Movimento uniforme

(COVEST-UFPE)– Em uma corrida de 400m, as posições dos dois primeiros colocados são, aproximadamente, funções lineares do tempo, como indicadas no gráfico abaixo. Sabendo-se que a velocidade escalar do primeiro colocado é 2% maior do que a do segundo, qual a velocidade escalar do vencedor?

Resolução:
A velocidade de cada corredor é dada pelas equações abaixo (1) e (2):

 

A velocidade do primeiro colocado é 2% maior que a do segundo colocado. Isso significa que é 100% (veloc. do segundo colocado) mais 2%. Portanto podemos escrever que:

(3)

Substituindo as equações (1) e (2) na equação (3) temos:

                                        

A velocidade escalar do vencedor será:

 

Resolução da prova mensal do 2º bimestre - 1ª série

A resolução da prova mensal sobre Movimento Uniforme está disponível no link abaixo:

Resolução da prova mensal do 2º bimestre - 1ª série

Chave elétrica

(UFMG)– Neste circuito, existem duas lâmpadas iguais, indica das por L, ligadas a uma pilha P, a um

amperímetro A, a um voltímetro V e a uma chave C, inicialmente aberta.
Considere os medidores ideais e constante a tensão elétrica fornecida pela pilha.

Fechando-se a chave C, as leituras dos medidores irão apresentar, em relação a seus valores iniciais,
a) aumento em A e diminuição em V.
b) aumento em A e o mesmo valor em V.
c) diminuição em A e aumento em V.
d) o mesmo valor em A e aumento em V.
e) os mesmos valores nos dois medidores.

Resolução:

1º) Com a chave aberta apenas uma das lâmpadas é percorrida pela corrente elétrica e o circuito fica reduzido conforme a figura abaixo:

Nesse caso a leitura do voltímetro será U e a leitura do amperímetro será I.

Considerando que a lâmpada possui uma resistência R, pode-se dizer que:

U = R. I      e   que    I = U/R

2º) Com a chave fechada, tem-se que considerar todo o circuito. Nesse caso as lâmpadas estão associadas em paralelo. Considerando que cada uma possui resistência R, a resistência equivalente fica igual a R/2. 
O voltímetro indicará a mesma leitura obtida com a chave aberta, pois em uma associação em paralelo os resistores possuem a mesma d.d.p. Lembre-se que a d.d.p. (diferença de potencial) depende dos potenciais dos pontos onde os terminais do resistor estão conectados. Como as duas lâmpadas estão ligadas a pontos coincidentes em termos de potencial, apresentam então a mesma tensão (ddp).
Quanto ao amperímetro há alteração em sua leitura, conforme pode-se observar abaixo:

Como I = U/R, pode-se afirmar que I₁= 2.I
Portanto a resposta correta está no item b.

Voltímetro

Determine para o circuito abaixo a indicação do voltímetro ideal V.

Resolução:
O voltímetro ideal não interfere no circuito, pois apresenta resistência infinita, fator este que impede a passagem de corrente elétrica por ele.
No esquema da figura o voltímetro está ligado aos terminais do resistor de 1,0 Ω. 
1º) Determinar a resistência equivalente aos resistores de 1,0 Ω e 3,0 Ω associados em paralelo.
      (produto/soma)

       Agora o circuito pode ser reescrito da seguinte forma:

2º) Determinar a intensidade da corrente elétrica utilizando a Lei de Pouillet:

3º) Determinar a tensão (d.d.p.) nos terminais do resistor equivalente aos resistores de  1,0 Ω e 3,0 Ω associados em paralelo, ou seja ao resistor de 3/4 Ω. Para tal devemos utilizar a primeira Lei de Ohm.                                          

Portanto a leitura do voltímetro é 3V.